Understanding Second Harmonic Generation: An intuitive introduction

In one of my recent laser projects, I am using a process called intracavity frequency doubling to obtain a powerful green laser beam from an infrared Nd:YAG laser. In the context of this project, I did a lot of research into frequency doubling (or second harmonic generation) which I want to present in the article below. It is more theoretical than my typical articles, but I hope it gives intuitive insight into one of the more complex topics a laser enthusiast might come across. Note that this text makes no claim to scientific completeness but exists rather as an introductory guide.

Let us start with linear media and then go into detail how nonlinear media give way to this fascinating process.

Linear media

Imagine an electromagnetic wave entering a linear medium. Since the electrons and protons in the atoms of the material are charged, they interact with the EM-wave. Specifically, they move in accordance with the electric field $\overrightarrow{\text{E}}$ , electrons against it (due to negative charge) and protons with it albeit much less due to their higher mass and thus inertia. The atom’s charges now don’t cancel out spatially and it turns into a (temporal) dipole. How much the electrons and protons move and thus how strong the dipole (= its dipole moment 𝑝) is, depends on the magnitude of $\overrightarrow{\text{E}}$ , but also on the atom itself, its polarizability α, which is simply p / $\overrightarrow{\text{E}}$. From α, other material constants can be deduced, such as the dielectric constant ϵ and the refractive index n. The polarizability contains $\overrightarrow{\text{E}}$, but does not include the response of the dipole, its own field $\overrightarrow{\text{E_d}}$. To include $\overrightarrow{\text{E_d}}$ and thus create a more macroscopic factor of how the atom responds to the applied field, the susceptibility χ is used – it takes into account $\overrightarrow{\text{E_d}}$ and the number of atoms within a unit volume of material (number density). χ describes how much a macroscopic material responds (polarizes) to an external $\overrightarrow{\text{E}}$:

ϵ₀ here is the vacuum permittivity that describes how strong of an electric field is induced in a vacuum by a unit electric charge and thus governs how charges like the mentioned dipoles create electric fields.

It is obvious that the polarization P is linearly correlated with $\overrightarrow{E}$. So, the incoming photon locally polarizes the material linearly with increasing light intensity, which gives linear media their name. The dipoles in the material oscillate with the same frequency as $\overrightarrow{E}$. The process of starting that oscillation takes energy from the light beam, attenuating it over distance. Once the dipoles are oscillating, they can stop by converting that energy e.g. in to heat.
Since the dipoles are associated with a moving charge (at the frequency of the light beam), it is also possible to convert that energy into light, of the same frequency of the incoming light, but a different direction and polarization. This incoherent process is called Rayleigh scattering.

Nonlinear media

The linear relationship described above is only an approximation of the real response of media based on the thought that the force bringing the electron back to its neutral position rises linearly with $\overrightarrow{E}$. This is very accurate for low magnitudes of $\overrightarrow{E}$ . For very high $\overrightarrow{E}$ such as in intense laser beams, the linear approximation becomes less true.
The force $F$_b that forces the electron back to its neutral point in the atom after being moved by the electric field is defined as follows:

φ is the electric potential that stems from the charge separation of the electron’s displacement and r is the displacement of the electron from its neutral point. This potential looks like this:

The solid curve is the real potential, the dashed one is the first order approximation. First order here refers to a Taylor Series approximation: Every curve can be approximated as a series of a sum of polynomials with increasing order. This can be a line (0^th order), but obviously a first order approximation (parabola) is much more fitting. Actually, a parabola happens to be a very good fit for small r. If one derives that parabola to get the force $F$_b , one receives a linear relationship. For bigger r, however, the approximation is not close enough to the real potential anymore and we need higher order approximations to correctly model the real behaviour.

So, the higher order terms not only exist in nonlinear media, they also do in linear media, but we don’t need to take them into account to accurately model their response. For the higher order terms to be necessary for correct modelling, to conditions need to be true:

a.     The field strength $\overrightarrow{\text{E}}$ needs to be very high.

b.     The material must be such that high r can be achieved with realistic values for $\overrightarrow{\text{E}}$, i.e. it must be responsive enough. This is expressed as higher-than-usual χ₂, χ₃, ...

Materials for which condition b is true are called nonlinear media. Usually, values for χ₁≫χ₂≫χ₃. This can be intuitively understood by looking at how a Taylor-Polynomial approximates a real function: Around the center, the first order approximation (the parabola) has, by far, the greatest influence on the graph’s behaviour, the second order only corrects it slightly, the third order corrects it by an even tinier amount. Since χ₂ is the highest non-linear term, this text will only regard this term. In the second order approximation,

One can see that the second order susceptibility is multiplied with E², which makes sense if you look up how Taylor-Polynomials are structured.

Let us now see what happens if the electric field is sinusoidal with a frequency ω, as is the case for light: $\text{E = E₀*sin⁡(ωt)}$ . Now:

The term $\text{E = χ₁E₀*sin⁡(ωt)}$ contains nothing surprising, it is just the linear response (scaling factor $\text{χ₁E₀}$ ) of the medium, containing the same frequency as the incoming light. The second order term however contains $\text{sin⁡(ωt)²}$. Since

The second order terms becomes

In the first equation, the polarization is time independent: A static electric field is built. The second term contains polarization that has double the frequency of the incoming light. This polarization can now start oscillating dipoles in the material that create electromagnetic radiation of that (doubled) frequency: light.

It is now clear that the response of the medium contains three parts: Linear response, static response (optical rectification) and the frequency doubled response, the latter of which can induce frequency doubled photons.

This is illustrated in the

picture to the left:

The incoming electric wave E (a) induces a polarization P (b) that is not just a linearly scaled version of E (c), but contains also a wave of double the frequency (d) and a static part (e).

Phase matching

If the conditions are correct, these SHG-photons are created everywhere in the medium. However, under normal conditions, the dispersion (wavelength dependence of the index of refraction n) of the medium results in every photon inside that medium having a photon of opposite phase somewhere, cancelling it out. This results in very low conversion efficiencies. Lets look at how this comes to be and how to solve that problem:

The frequency-doubled photons that are created in the medium usually dont start with the phase that the fundamental wave had at that point, but there is a fixed relationship: If the phase of the fundamental wave is t, the phase of the SHG-wave is 2t. In a medium with no dispersion, meaning no wavelength dependence of n, this leads to the created waves always constructively interfering. To illustrate this, consider the following picture: At point a, the phase of the fundamental sine wave is zero, so its amplitude is also zero. This means that the cosine wave has a phase of 2*0=0, so it has an amplitude of 1. At point b, the fundamental's phase is π/2, so its amplitude is 1. The cosine wave's amplitude is 2*π/2=π, with an amplitude of -1, same as the -just created- cosine wave 2. Continuing this, you can see, that all the waves constructively interfere, since they are in phase. This is of course assuming that the waves move with the same speed $\text{ν_ω = ν _2ω}$, i.e. the frequency has no influence on the way the wave travels through the medium.

In reality however, the speed of the wave is dictated by the index of refraction n, which depends on the light’s frequency: Higher frequencies mean higher indices of refraction mean slower propagation speed ν. The index of refraction actually is defined by how much slower light travels through the medium in comparison to vacuum, e.g. n=2 would mean that a photon moves half the speed as it would in vacuum.

In a real medium like that the frequency doubled waves still start with the same amplitude as the ones in the fictive medium, but they don’t all have the same phase – over some distance their relative phase shifts. At some distance that phase shift will reach -90° and the created wave will destructively interfere with the first created wave and the amount of frequency light starts dropping. This length is called coherence length (Not to be confused with the coherence length of lasers!). In the illustration above, that distance is a-f.

For optical frequencies, the coherence length is on the order of magnitude of 10 μm. Theoretically, destructive interference could be fundamentally avoided by cutting a crystal shorter than that but this is difficult to achieve technically and also not desirable since there would not be enough crystal length to convert much of the incoming light. So, if a meaningful amount of light is to be extracted, the effect of the dispersion needs to be counteracted by equalizing the indeces of refraction n_ω and n_2ω. The process of doing that is called phase matching. In isotropic media, since the indeces of refraction for different wavelengths can never be the same, phase matching is not possible. However, it is possible to equalize two n_ω and n_2ω in birefringent media, since these have two indeces of refraction depending on polarization and propagation direction. There are two broad types of techniques used for phase matching: Critical and non-critical phase matching. In critical phase matching, the angle of the crystal compared to the light’s polarization is critical, in non-critical phase matching it is not – the equalization of index of refraction is done via different means, e.g. temperature.

Critical phase matching

In critical phase matching, the angle of a birefringent crystal is tuned such that n_ω= n_2ω. The key to understanding how that is possible is understanding the influence of birefringence on the refractive index.

Uniaxially birefringent media have a so-called optical axis. Photons that have their polarization (here, we assume linear polarization) perpendicular to that axis move with a different speed, i.e. experience a different refractive index than photons that have their polarization parallel to the optical axis. Specifically, photons with polarization perpendicular to the optical axis will experience the ordinary refractive index n_o, photons with polarization parallel to it will experience the extra-ordinary refractive index n_e. In positively birefringent media, n_e > n_o, in negatively birefringent media, n_e < n_o. Let us look at some examples on how this works for beams with different directions and polarisations:

Here, you can see three light beams with two types of polarisations travelling at different directions relative to the ordinary axis (here assumed to be the z-axis of the medium). On the left side, the refractive index is considered for these beams. It is immediately apparent that the second type of polarization doesn’t change direction when the beam is turned and thus always sees the same refractive index n_o. The first polarization, though, does change direction: At 45° it is partly along the x- and z-Axis which means the refractive index will be somewhere between n_o and n_e. At 90° it is completely along the z-Axis, so it refractive index is n_e.

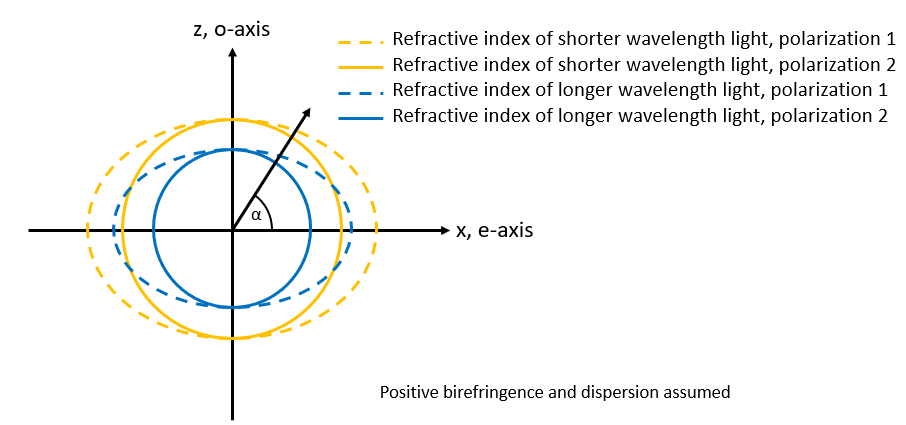
This dependence of direction and polarization can be graphed in a so-called index ellipsoid. This is shown below, for a positively birefringent medium, so n_e>n_o. For the polarization along the y-axis (see pol. 2 above) the index-ellipsoid is a circle since the refractive index is independent of the angle.

I have also taken the freedom to, in preparation for the next step, add the index-ellipsoid for shorter wavelength light, like the frequency doubled light would be. Under normal dispersion, the refractive index is larger for shorter wavelengths, so the index ellipsoid is just scaled up.

We are now in the final steps of understanding critical phase matching! Lets see what happens, when the fundamental mode photons have the same polarization, lets say pol. 1 (extra-ordinary polarization). If phasematching is to occur, the refractive indeces need to be the same. Looking at the graph above, the blue dotted curve can only possible intersect with the orange solid curve. This means, that with the correct crystal angle two extraordinary photons can efficiently create an ordinary polarized photon. This is called Type 1 critical phase matching.

This insinuates that there other types – and indeed there are. If two fundamental mode photons with different polarization (ordinary and extra-ordinary) are considered, their average index lies in between n_o and n_e, so their index ellipsoid is between the solid blue and dotted blue line in the graph above. Here, it is again possible, that this ellisoid is intersected with the solid orange one, meaning the two photons again create an ordinary polarized photon. This is type 2 – critical phase matching. This can be quite confusing and is better shown visually – so please consider the graph below, where the two types are visualised.

It is also apparent that two identically polarized photons cannot efficiently create a photon with the same polarization since the index ellipsoids (or circles in the case of ordinarily polarized photons) never touch, i.e. no perfect phase matching is possible. This process, also called Type 0 critical phase matching, is only possible to achieve in very short crystals (see “coherence length” above) or in so-called periodically poled non-linear crystals. Describing this process however would be too much for this article. Similarly, there are more methods for avoiding the problems introduced by dispersion but since critical phase matching is most commonly used in typical solid state lasers, we’ll stop here and finish the chapter of phase matching.

Let us now, in this final short section recall what we have covered: High intensity light can, in nonlinear media, create significant deviations of the electrons from their rest potential. Their oscillations can now not fully follow the fundamental electric field, leading to a linear combination of different frequency components, one of them leading to the creation of photons with double the frequency of the fundamental light. However, dispersion ruins the efficiency of this process in real media through a phase mismatch of the created photons leading to destructive interference. To match the phases of the created photons, their speed (and thus their corresponding refractive index) needs to be matched with the speed of the fundamental wave. This can be done using birefringent media in the case of critical phase matching.

With this knowledge, a laser engineer (or enthusiast!) is armed with the necessary basic tools to build simple laser systems involving second harmonic generation and provides a good starting point for further research on this topic.

I hope this text was useful to you, and perhaps de-mystified some of the terms and connections behind SHG for you. Thank you so much for reading!

~Nik